剑指 Offer 14- I. 剪绳子

Posted on | In ,

题目

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

1
2
3
4
5
6
7
8
9
10
示例 1：

输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:

输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36

题解

这里就自己手动算了几个值；

1 是没法分的
2 可以分为 1 和 1    积为 1
3 可分为 1 和 2         积为 2 
4 可分为 (2,2),(1,3) 最大积为4
5 可分为(1,4),(2,3)    最大积为 6
6 可分为(1,5)(2,4),(3,3)    最大积为9

虽然可以分为多个但是多个也是由几个值加在一起的。比如分的时候分出来了5以上那么一定会把他再分。而前期算出来了每个值的最大值都可以后面再利用。

比如再计算7，它可分为(1,6)(2,5)(3,4);
虽然其中5和6还可以再分。但此时我们就不管它分不分了，直接在上面查表。
发现5分之后的最大值是6，6分之后的最大值是9；
明显这是比5或6在原来的贡献更大，并且已知是他所能分开的最大贡献了。于是后面维护这个表就好了。

当然还有别的更好的算法吧。但这个是可以求得结果的。

HashMap

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public int cuttingRope(int n) {
    HashMap<Integer, Integer> integerIntegerHashMap = new HashMap<>();
    integerIntegerHashMap.put(1,1);
    integerIntegerHashMap.put(2,2);
    integerIntegerHashMap.put(3,3);
    integerIntegerHashMap.put(4,4);
    if (n < 5){
        if (n == 2){
            return 1;
        } else if (n == 3){
            return 2;
        } else if (n == 4){
            return 4;
        }
    }
    for (int i = 5 ; i <= n ; i ++){
        int MAX = 0;
        for (int j = 1; j <= i/2 ; j++){
            int temp = integerIntegerHashMap.get(j) * integerIntegerHashMap.get(i-j);
            if (temp > MAX){
                MAX = temp;
            }
        }
        integerIntegerHashMap.put(i,MAX);
    }
    return integerIntegerHashMap.get(n);
}

数组：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int cuttingRope(int n) {
        if (n < 5){
            if (n == 2){
                return 1;
            } else if (n == 3){
                return 2;
            } else if (n == 4){
                return 4;
            }
        }
        int[] ints = new int[n + 1];
        for (int i = 1; i<5; i++){
            ints[i] = i;
        }
        for (int i = 5 ; i < ints.length ; i ++) {
            int MAX = 0;
            for (int j = 1; j <= i / 2; j++) {
                int temp = ints[j] * ints[i - j];
                if (MAX < temp) {
                    MAX = temp;
                }
            }
            ints[i] = MAX;
        }
        for (int i = 1; i < ints.length; i++){
            System.out.println(ints[i]);
        }
        return ints[n];
    }
}

分别写了下hashmap和数组，结果HashMap高一点点

看答案

看到了一个挺好的动态规划。他把剪绳子分成了两种。眼下手里已经剪了的部分乘上剩下部分；剩下部分有两种命运：

  1. 不剪了；
  2. 接着剪；他要从里面选较大的那个；

我们发现任何大于 3 的数都可以拆分为数字 1，2，3的和，且它们对 3 的余数总是 0，1，2，因此我们可以仅用 dp[0]，dp[1]，dp[2] 表示所有大于 3 的值，这样空间复杂度可降到 O(1)。

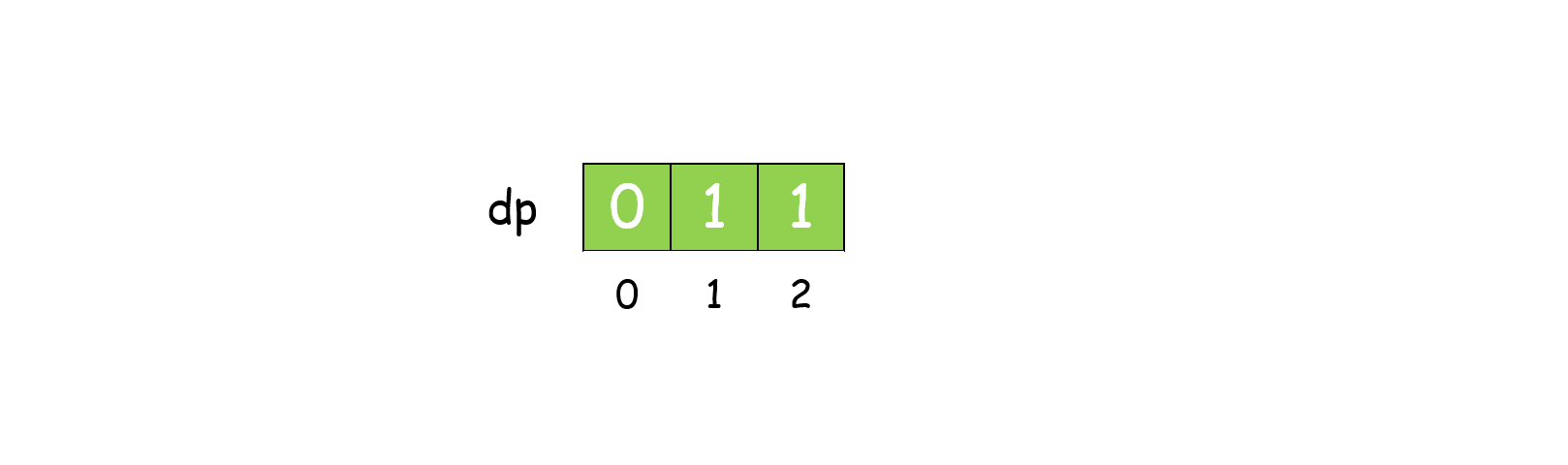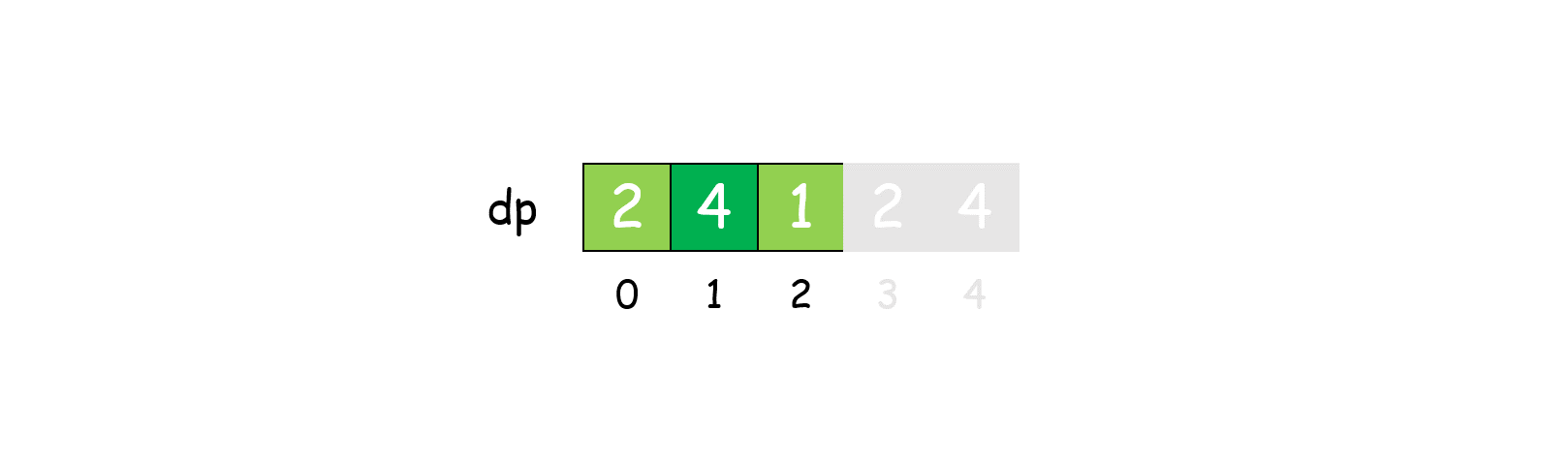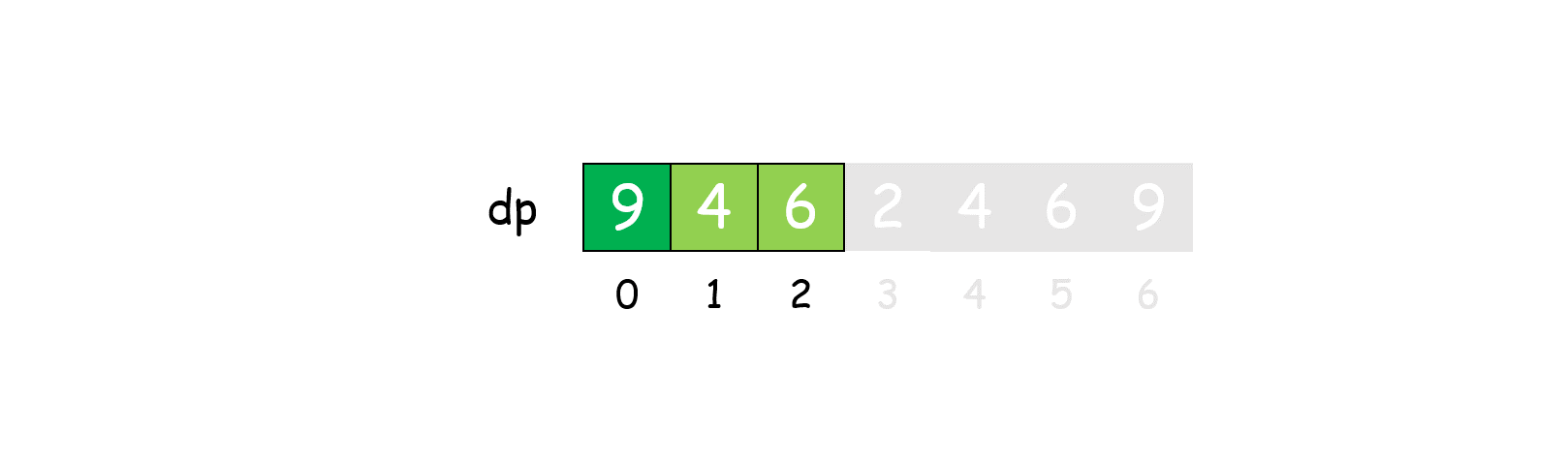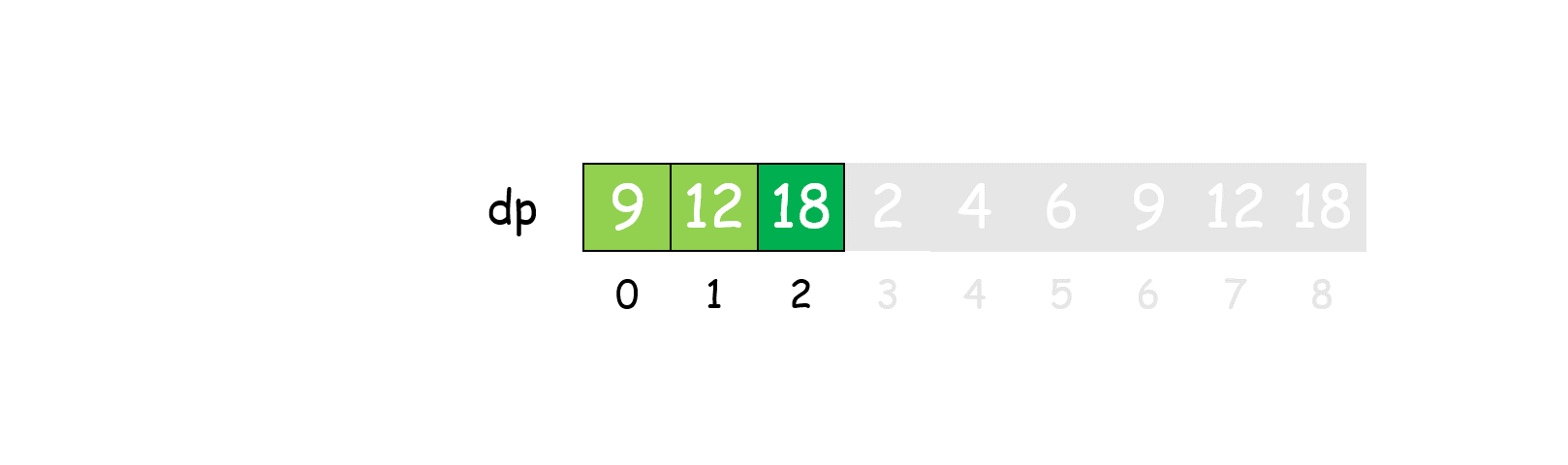
14.gif

1
2
3
4
5
6
7
8
class Solution:
    def cuttingRope(self, n):
        dp = [0, 1, 1]
    for i in range(3, n + 1):
        dp[i % 3] = max(max(dp[(i - 1) % 3], i - 1),
                2 * max(dp[(i - 2) % 3], i - 2),
                3 * max(dp[(i - 3) % 3], i - 3))
    return dp[n % 3]