左神算法-基础课-05

Posted on | In , , ,

题目一 认识哈希函数和哈希表

哈希函数

一、性质

  1. 哈希函数的输入域是无限大的；
  2. 哈希函数的输出域是有穷尽的；
  3. 输入如果一样，输出一定一样；
  4. 哈希碰撞：输入不一样，也可能得到输出一样的值；（因为输入域无穷大，输出域有限大，所以必然会产生冲突；)
  5. 哈希函数的离散性：也就是输出域每个值被输出的概率都差不多一样大；

二、特征

  1. 输出的值和输入没有关系；保证它结果是均匀出现的；

三、找到一千个独立的哈希函数

独立的意思在于一个哈希函数不会随着一个的变化而变化；

具体做法：

一个哈希函数可以生成16位的十六进制的输出集；他们每个位的码都是相互不关联的；

那么可以把它前八位作为一个哈希函数$h_1$，后八位做一个哈希函数$h_2$

紧接着，$h_3 = h_1+1*h_2$ ；这里第三个哈希函数与他们两个是没有关系的；

以此类推： $h_i=h_1+(i-2)*h_2$ 做出很多很多的哈希函数，并且它们相互之间是相互独立的；

四、 粗略介绍哈希函数的内部构造

比如说一个字符串，不管多长，要把它得到一个16位的哈希函数；

就分割16位16位的异或，再错位异或之类的；

实现方法有很多；

哈希表

哈希表可以： put(key1, value1)，get(key1)，remote(key1)

一、哈希表的存放

比方有一个数组大小是 N，进来一个(key, value) ;

通过计算 key的哈希值，膜上数组的大小 N ; 可以在数组中找到一个存放这个(key, value) 的位置；以节点的形式把它存放在数组中；

再有值进来冲突了某个位置，就在节点后形成链表的形式；

二、哈希表的扩容

某一个位置的链很长了，那么就把它扩容；扩容讲究也很宽泛。可以成倍扩容；那么存放N个元素可能就要扩容 $log_2N$次

离线扩容：指的是在用的哈希表已经很元素很多了，那么想办法先让访问都在目前的哈希表上访问；然后再后台再扩容的空间里把元素放进来。等做好后就把访问引到这个上面来；它扩容过程不占用线上访问时间；

哈希函数的一个使用场景

【面试题】：给你一个大文件，100T，寸的都是数字；把其中所有数字得到一个新文件，保证每个数不重复；

给1000个机器；为了充分使用这1000个机器，可以用哈希函数来给1000个机器来分流。每从大文件中读书来一个数，就算出它的哈希函数。然后再膜上1000，决定它该由哪个机器处理。这样做有个好处就是相同的数会被分配到同一个机器上去；这样重复的值就可以被找到；

大数据的题目：就用哈希函数，相同输入导致相同输出。不同输入均匀分布；

题目二 设计RandomPool结构

题目

设计一种结构，在该结构中有如下三个功能：

  • insert(key)：将某个key加入到该结构，做到不重复加入。
  • delete(key)：将原本在结构中的某个key移除。
  • getRandom()： 等概率随机返回结构中的任何一个key。

【要求】Insert、delete和getRandom方法的时间复杂度都是 O(1)

思想

前两个方法是可以考虑用一个哈希表来自然实现的；但是第三个单纯用一个哈希表是得不到的；

所以这里除了原本的哈希表还需要另外的结构来辅助完成这个功能；

  1. 在不考虑delete的情况，仅仅往哈希表里的加入元素：

    我们要知道加入了几个了

    第一个哈希表加入第一个元素(key,value)，另一个哈希表加入（value，key），value表示第几次插入到这个哈希表中；

    我们在第一个哈希表中可以根据key找到它是第几个插入的；在第二个可以通过第几个插入的找到key值；

    str0 —— 0 0 —— str0

    str1 —— 1 1 —— str1

    str2 —— 2 2 —— str2

    strN —— N N —— strN

    以此类推，加入N个后，可以在 0 ~ N-1之间随机选择一个数在第二个哈希表找到key，再在第二个哈希表中找到相对应的值；这种情况下，可以根据加入元素多少实现等概率返回。

  2. 删除情况：

    比方要删除 0 ~ N-1 中的某一个数。可以在第一个哈希表中找到它是第几个加入的。相对应的加入的元素数目也减少了；但是在随机的时候就可能随机到 i。另外由于总数变为 N-1了，随机范围是 0 ~ N-2了，所以之前最后一个加入的次序为 N-1 的元素就随机不到了。所以可以用最后一个加入的这个元素补被删除的那个位置。

    另外这里的进入哈希表的次序只不过是一个辅助信息。它在接口中，不对外呈现；所以更改它没有多大影响；

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public static class Pool<K> {
    private HashMap<K, Integer> KeyIndexMap;
    private HashMap<Integer, K> IndexKeyMap;
    private int size;

    public Pool() {
        this.IndexKeyMap = new HashMap<Integer, K>();
        this.KeyIndexMap = new HashMap<K, Integer>();
        this.size = 0;
    }

    public void insert(K key) {
        if (!this.KeyIndexMap.containsKey(key)) {
            this.KeyIndexMap.put(key, size);
            this.IndexKeyMap.put(size ++ , key);
        } else {
            System.out.println("Already exits!");
        }
    }

    public void delete(K key) {
        if (this.KeyIndexMap.containsKey(key)) {
            int deleteIndex = this.KeyIndexMap.get(key);
            int lastIndex = --this.size;
            K lastKey = this.IndexKeyMap.get(lastIndex);
            this.KeyIndexMap.put(lastKey, deleteIndex);
            this.IndexKeyMap.put(deleteIndex, lastKey);
            this.KeyIndexMap.remove(key);
            this.IndexKeyMap.remove(lastIndex);
        } else {
            System.out.println("SomeThing Wrong!");
        }
    }
    public K getRandom() {
        if (this.size == 0) {
            return null;
        }
        int randomIndex = (int) (Math.random() * this.size); // 0 ~ size - 1
        return this.IndexKeyMap.get(randomIndex);
    }

}

在序列中出现了洞，用最后一个去填是常规操作

题目三 认识布隆过滤器

场景

假设有一个需求：100亿个url黑名单；每个url是64字节；使用场景是，给一个 url 如果这个 url 属于黑名单，那就返回 true， 否则返回 false；

这种场景用哈希表的话就需要把所有的东西加入到内存当中来；这样子所需的内存资源就很多很多。所以就可以用布隆过滤器；

布隆过滤器有一个缺点：它有一定的失误率（宁可错杀3000不可放过一个；在黑名单的不会弄错，他会返回 True；但是不在黑名单的有一定的概率会搞错。）

  1. 布隆过滤器需要先准备一个长比特数组，它的长度为 $m$ ；使用这个长比特数组的目的就在于我们准备用其中某几个 bit 的位置来组合说明某个url是否存在；

    • 长比特数组的实现
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    public static void main(String[] args) {
        // 一个整数的位数是 32个bit，那么申请的整数数组是 32000 bits
        int[] arr = new int[1000];

        int index = 30000;  // 把第 30000 个位置描黑

        int intIndex = index / 32;    // 它在整数数组里的位置

        int bitIndex = index % 32;  // 在所在的整数里的哪一个 bit 位；

        arr[intIndex] = (arr[intIndex] | (1 << bitIndex));  // 把arr[intIndex] 这个整数的 第bitIndex位描黑
    }

  2. 针对每个 url 我们把它经过 $k$ 个独立的哈希函数，算出 $k$ 个哈希值，再膜上比特数组的长度 $m$ 得到比特数组的 $k$ 个位置 ；分别在数组上把这 $k$ 个位置给描黑（写上1）；

  1. 查询：来了一个 url ，用它经过我们之前的 $k$ 个哈希函数，同样的方法求出来 $k$ 个位置；看比特数组中这 $k$ 个位置是否被描黑了；如果都被描黑了，则我们可以认为这个 url 在黑名单里（有可能有失误，碰巧那几个都被涂黑了。）。如果有一个不是黑的，则它绝对不在黑名单了；

    • 所以选择哈希函数的 $k$ 的大小，和比特数组长度 $m$ 来控制失误率；

      • $m$ 越大，失误率降低；$m$ 越小，失误率升高；下面是 $m$ 的所需公式 ：$n$ 表示样本量；$p$ 是预期失误率；
      • 确定哈希函数个数 $k$ 的个数：这个数是小数需要向上取整
  • 当哈希函数个数 $k$ 和样本数 $m$ 确定时（都向上取整了），预期失误率是：
    $$
p=(1-e^{-\frac{n*k}{m}})^k
$$

题目四 认识一致性哈希

场景

经典服务器抗压结构：后端集群有 $N$ 台机器；前端获取请求后根据请求的 $key$ 来得到一个哈希值。 然后在得到这个哈希值除以 $N$ 的余数；根据这个余数把这个请求分配到相对应位置的机器上。这样会使得几台机器得到的请求压力差不多相同。（负载均衡）

但是当需要在这个结构中加机器或者减机器的时候这个结构就需要大范围的改动。因为每一个key的哈希值会根据新的机器数和之前得到的位置是不同的。（数据归属变化了）

这种情况下就可以使用一致性哈希。它可以把数据迁移代价变得很低，又负载均衡；

过程

image-20201210152321153

实际服务器集群的结构：

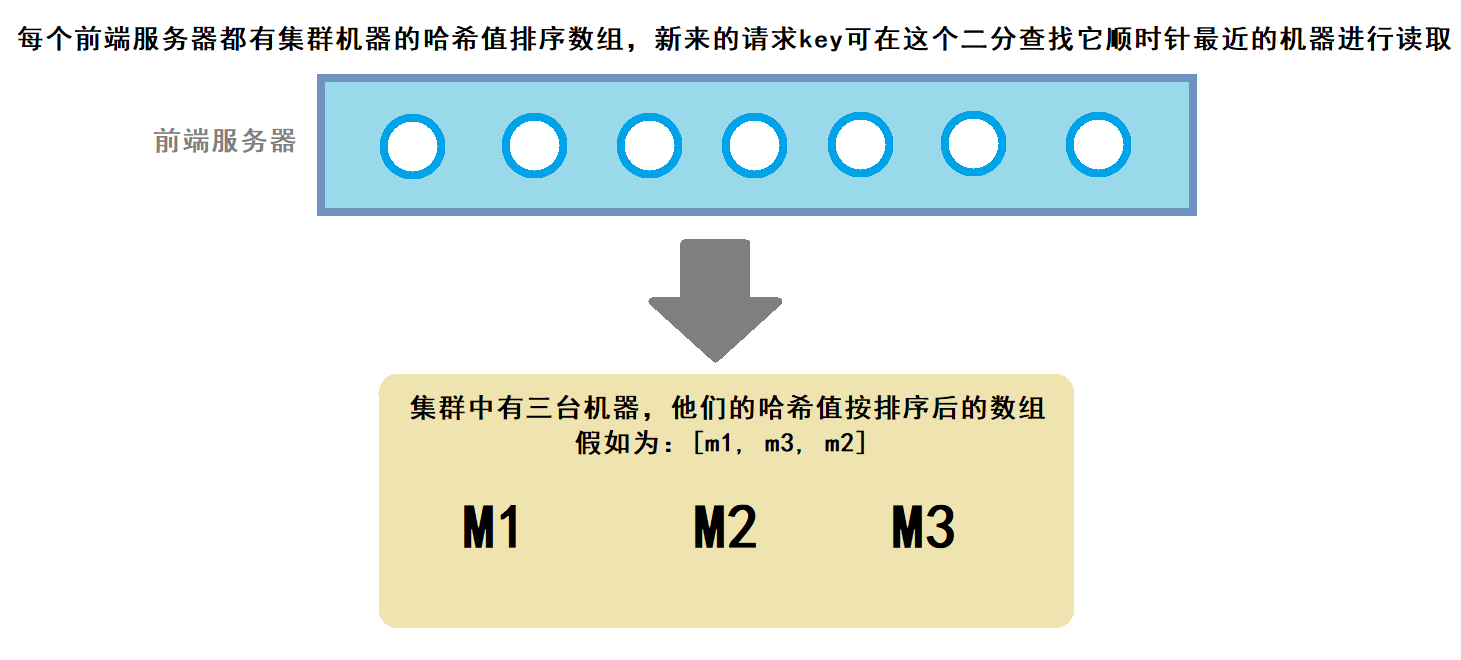
image-20201210153820881

此时需要加入新的机器

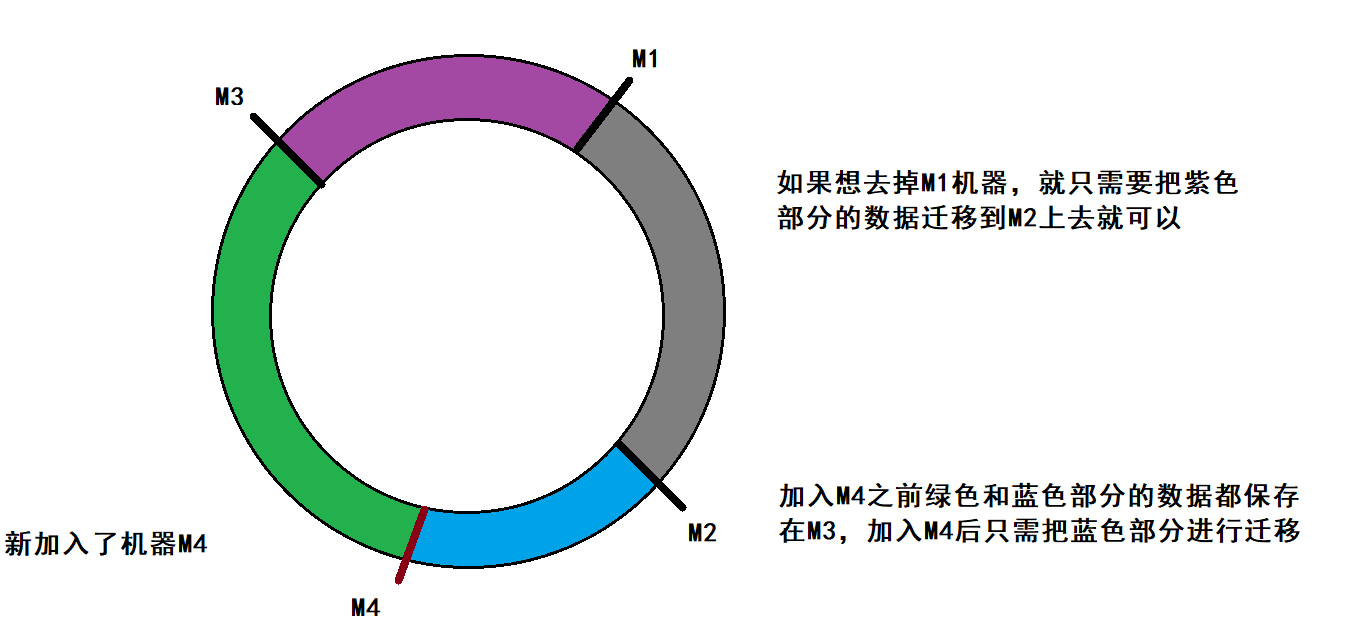
image-20201210160021986

缺陷

  • 在机器数量比较小的时候，他们在哈希值组成的环中的分布不是均分的；使得某个机器可能负载过多；
  • 即使人为的让他分布均匀，但是再加入新机器时；还是会破环原来的均衡；

这里我们可以用虚拟节点技术来解决这个问题；

虚拟节点

每个物理机器不再使用自己的ip信息来分配哈希域的区间

image-20201210170417902

题目五 岛问题

题目

一个矩阵中只有0和1两种值，每个位置都可以和自己的上、下、左、右 四个位置相连，如果有一片连在一起，这个部分叫做一个岛，求一个矩阵中有多少个岛？

举例：

0 0 1 0 1 0

1 1 1 0 1 0

1 0 0 1 0 0

0 0 0 0 0 0

这个矩阵中有三个岛。

思想

单任务的想法：

  • 遇到岛就深度遍历把遍历过的都给标记起来。之后遇到标记过的，直接跳过，直到遇到未标记的岛，就给岛的数量加一；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public static int countIslands(int[][] m) {
    if (m == null || m[0] == null) {
        return 0;
    }
    int N = m.length;
    int M = m[0].length;
    int res = 0;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            if (m[i][j] == 1) {
                res ++;
                infect(m, i, j, N, M);
            }
        }
    }
    return res;
}

public static void infect(int[][] m, int i, int j, int N, int M) {
    if (i < 0 || i >= N || j < 0 || j >= M || m[i][j] != 1) {
        return ;
    }
    m[i][j] = 2;
    infect(m, i + 1, j, N, M);
    infect(m, i - 1, j, N, M);
    infect(m, i, j + 1, N, M);
    infect(m, i, j - 1, N, M);
}

多任务的思想（并行计算）：

  • 把矩阵分块处理分别数出其中各自有多少岛屿
  • 然后对矩阵块的边缘进行考虑
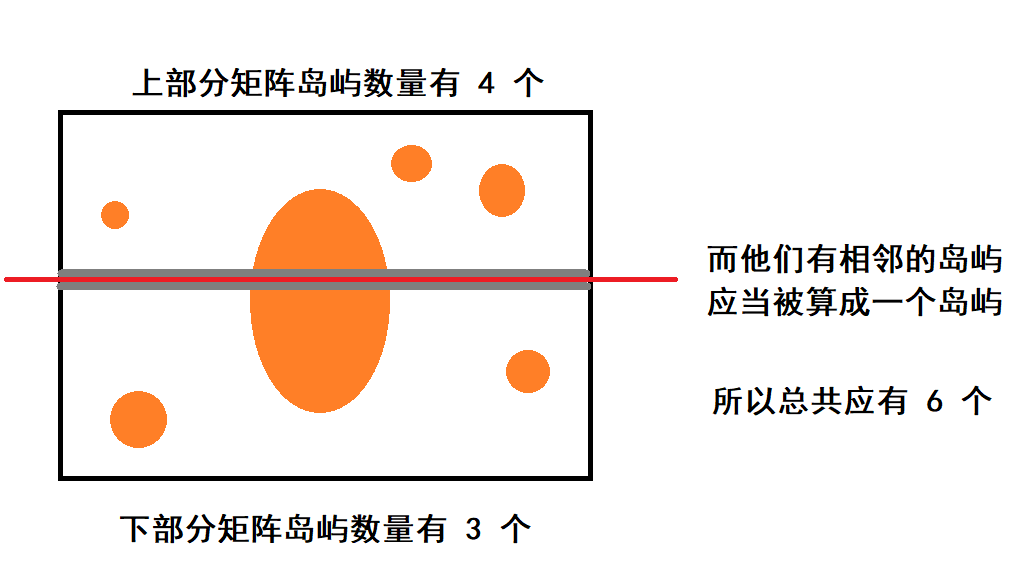
    • 普遍情况下要对矩阵间的边缘也就是 灰色部分进行考察；两个矩阵边缘相连，在不同情况下是不同的，在下图中两个边缘区域相连，他们总岛屿数 - 1；image-20201211162620873
  • 考虑矩阵块边界相连时，把各个矩阵块里找到的岛屿当作并查集；
  • 搜索边界，如果分属于两个矩阵块里的岛屿（并查集）在边界是相连的但是没有被合并过，那么总岛屿数减一，把他们相连；

题目六 并查集

概念好理解，但是比较难的是在什么场合去应用他。

可应用的地方

  • 检查两个元素是否属于一个集合：
    • isSameSet(A, B) ：
  • 两个元素各自所在的集合合并在一起：
    • set union(element A, element B)

并查集的结构

并查集的初始化

初始化时需要把所有的元素都给出；并每个元素都可以被看成是独立的集合；它有一个自旋指向；

并查集代表一个集合的节点会把指针指向自己；可以通过指针指向自己的节点识别出集合的头。

image-20201211095208875

并查集合并

两个集合合并时任意的让其中一个集合的代表节点解除自旋指向，指向另一个并查集中的节点：

一般会让节点数更小的，指向节点多一些的并查集。

image-20201211095510716

检查元素是否在一个集合：就是找到两个节点一直找到他们所在集合的代表节点，看他们是否是一个节点；

并查集的优化

查询后再优化，仅优化查询路径上的节点

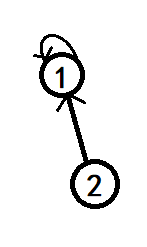
查询 $4$ 节点会路过三个节点，直到找到 $1$ 节点

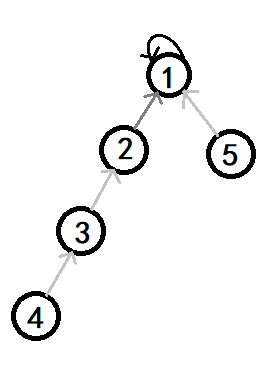
image-20201211100851717

然后再把这个结构进行优化成这个样子：

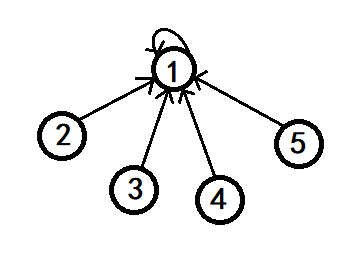
image-20201211101606972

至于那些指向 $4$ 或者 $3$ 和 $2$ 的都保持原地不动。仅仅把查询 $4$ 到代表节点的路径扁平化，让它们指向 $1$ 节点；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
public static class Node {
    // whatever you like
}

public static class UnionFindSet {
    public HashMap<Node, Node> fatherMap;
    public HashMap<Node, Integer> sizeMap;

    public UnionFindSet() {
        fatherMap = new HashMap<Node, Node>();
        sizeMap = new HashMap<Node, Integer>();
    }

    public void makeSets(List<Node> nodes) {
        fatherMap.clear();
        sizeMap.clear();
        for (Node node: nodes) {
            fatherMap.put(node, node);
            sizeMap.put(node, 1);
        }
    }

    private Node findHead(Node node) {
        Node father = fatherMap.get(node);
        if (father != node) {
            father = findHead(father);
        }
        fatherMap.put(node, father);
        return father;
    }

    public boolean isSameSet(Node a, Node b) {
        return findHead(a) == findHead(b);
    }

    public void union(Node a, Node b) {
        if (a == null || b == null) {
            return;
        }
        Node aHead = findHead(a);
        Node bHead = findHead(b);
        if (aHead != bHead) {
            int aSetSize = sizeMap.get(aHead);
            int bSetSIze = sizeMap.get(bHead);
            if (aSetSize <= bSetSIze) {
                fatherMap.put(aHead, bHead);
                sizeMap.put(bHead, aSetSize + bSetSIze);
            } else {
                fatherMap.put(bHead, aHead);
                sizeMap.put(aHead, aSetSize + bSetSIze);
            }
        }
    }

时间复杂度

所有的操作包括：查询过程 + 合并过程 ——> $O(N)$ 及以上，那么平均每次操作都是常数级别，可以说是：$O(1)$

应用：岛问题