左神算法-基础课-03

Posted on | In , , ,

题目一：用数组结构实现大小固定的队列和栈

栈与队列的数据结构都是很熟悉的了；

栈

具体在这里他们的实现：栈的实现涉及：压栈，出栈，返回栈顶元素，返回栈元素个数等等；在栈满时压栈会报错；在栈空时出栈会报错；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public static class ArrayStack {
    private Integer [] arr;
    private Integer size;
    public ArrayStack(int initSize) {
        if (initSize < 0){
            throw new IllegalArgumentException("The init size is less than 0");
        }
        arr = new Integer[initSize];
        size = 0;
    }

    public Integer peek() {
        if (size == 0){
            return null;
        }
        return arr[size - 1];
    }

    public void push(int obj) {
        if (size == arr.length){
            throw new ArrayIndexOutOfBoundsException("The Stack is full");
        }
        arr[size++] = obj;
    }

    public Integer pop() {
        if (size == 0){
            throw new ArrayIndexOutOfBoundsException("The stack is empty");
        }
        return arr[--size];
    }
}

队

另外的是队列的实现；一般普通的方法是维护队头和队尾两个变量。左神在这里引入了第三个变量：size，也就是队列中元素的个数；

如果size是数组的大小的话，那么就不能从队尾入队了，如果小于数组的大小，则可以入队；

如果size是0的话，就不能从队头出队；如果大于0，就可以从队头入队；

这样对于入队与出队的操作就只需要看size就可以；队头和队尾两个变量就没有关系了；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public static class ArrayQueue {
    private Integer [] arr;
    private Integer size;
    private Integer first;
    private Integer last;   // 指向队尾的后一格（可能空，也可能不空）
    public ArrayQueue(int initSize) {
        if (initSize < 0){
            throw new IllegalArgumentException("The init size is less than 0");
        }
        arr = new Integer[initSize];
        size = 0;
        first = last = 0;
    }

    public Integer peek() {
        if (size == 0){
            return null;
        }
        return arr[first];
    }

    public void push(int obj) {
        if (size == arr.length){
            throw new ArrayIndexOutOfBoundsException("The queue is full");
        }
        size++;
        arr[last] = obj;
        last = last == arr.length - 1 ? 0 : last + 1;
    }

    public Integer poll() {
        if (size == 0){
            throw new ArrayIndexOutOfBoundsException("The stack is empty");
        }
        size --;
        int tmp = first;
        first = first == arr.length - 1 ? 0 : first + 1;
        return arr[tmp];
    }
}

【思考】如果没有size该如何实现

如果没有size则在队为空时，队头 start 和队尾 end 都指向一个位置；

入队时要判断是否还有空间，则就是 end 的下一个位置如果不是start 就说明可以入队；这里 end 的下一个位置分为两种情况，end到达数组尾部，他的下一个位置是0，end未到达数组尾部，他的下一个位置是 end + 1；

出队时要判断是否队为空，则就是 start 和 end相等；

题目二：实现栈，并且实现返回栈中最小元素的操作

image-20201024110123120

【实现】：这个栈有两个数组，一个数组是 data 数组，另一个数组是 min最小值数组；

在往data和min是两个同步运作的数组；

data入栈，min也入栈：data入栈一个数字 x，则把这个数字与min的栈顶比较，把较小值入min栈；当然如果min为空，则直接入栈就好了；

data出栈，min也出栈：这个没得说，他们的个数是一样的；

实现一：最小栈与数据栈同步

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public static class MyStack2 {
    private Stack<Integer> stackData;
    private Stack<Integer> stackMin;

    public MyStack2() {
        this.stackData = new Stack<Integer>();
        this.stackMin = new Stack<Integer>();
    }

    public void push(int newNum) {
        if (this.stackMin.isEmpty()){
            this.stackMin.push(newNum);
        } else if (newNum < this.getmin()){
            this.stackMin.push(newNum);
        } else {
            int newMin = this.stackMin.peek();
            this.stackMin.push(newMin);
        }
        this.stackData.push(newNum);
    }

    public int pop() {
        if (this.stackMin.isEmpty()) {
            throw new RuntimeException("Your Stack is empty");
        }
        this.stackMin.pop();
        return this.stackData.pop();
    }

    public int getmin() {
        return this.stackMin.peek();
    }
}

实现二：最小栈与数据栈不一定同步

之前两个栈是同步的过程；而当进来的数大于当前最小值时的过程可以通过判断不用往最小栈里添加。弹出栈时，当当前栈中最小值被弹出了，最小栈才做改变。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public static class MyStack1 {
    private Stack<Integer> stackData;
    private Stack<Integer> stackMin;
    public MyStack1(){
        this.stackData = new Stack<Integer>();
        this.stackMin = new Stack<Integer>();
    }
    public void push(int newNum) {
        if (this.stackMin.isEmpty()){
            this.stackMin.push(newNum);
        } else if (newNum <= this.getmin()){
            this.stackMin.push(newNum);
        }
        this.stackData.push(newNum);
    }
    public int pop() {
        if (this.stackData.isEmpty()) {
            throw new RuntimeException("Your stack is empty.");
        }
        int value = this.stackData.pop();
        if (value == this.getmin()){
            this.stackMin.pop();
        }
        return value;
    }

    public int getmin() {
        if (this.stackMin.isEmpty()) {
            throw new RuntimeException("Your stack is empty.");
        }
        return this.stackMin.peek();
    }
}

题目三：用队列实现栈，用栈实现队列

image-20201024112244638

用队列实现栈结构

需要两个队列；

一个数据队列 data，一个辅助队列 help ；

入队就把数据放进 data；

弹出时需要弹出进入 data 的最后一个元素；所以需要把队列前面的元素出队放入 help 当中；得到和栈一样的结果；

但此时的 help 成了 data 的作用，所以把他们的引用交换一下就可以；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public static class TwoQueuesStack {
    private Queue<Integer> queue;
    private Queue<Integer> help;
    public TwoQueuesStack() {
        queue = new LinkedList<Integer>();
        help = new LinkedList<Integer>();
    }
    public void push(int pushInt) {
        queue.add(pushInt);
    }

    public int peek() {
        if (queue.isEmpty()) {
            throw new RuntimeException("Stack is empty!");
        }
        while (queue.size() != 1) {
            help.add(queue.poll());
        }
        int res = queue.poll();
        help.add(res);
        swap();
        return res;
    }

    public int pop() {
        if (queue.isEmpty()) {
            throw new RuntimeException("Stack is empty!");
        }
        while (queue.size() != 1) {
            help.add(queue.poll());
        }
        int res = queue.poll();
        swap();
        return res;
    }

    private void swap() {
        Queue<Integer> tmp = help;
        help = queue;
        queue = tmp;
    }
}

用栈实现队列

需要两个栈；

push 栈 和 pop 栈

往 push 栈里加入数据；若想得到该队列的出队。则需要从 push 栈中把所有数据倒到 pop 栈中；从pop 栈栈顶返回；

倒数据有两个规则：

1）push 栈往 pop 栈里倒数据要一次性倒完；不要有剩余；

2）如果 pop 栈不为空，那么push 栈一定不要倒；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public static class TwoStacksQueue {
    private Stack<Integer> stackpush;
    private Stack<Integer> stackpop;

    public TwoStacksQueue(){
        stackpush = new Stack<Integer>();
        stackpop = new Stack<Integer>();
    }
    public void push(int pushInt) {
        stackpush.push(pushInt);
    }

    public int poll() {
        if (stackpush.empty() && stackpop.empty()) {
            throw new RuntimeException("Queue is empty!");
        } else if (stackpop.empty()){
            while (!stackpush.empty()) {
                stackpop.push(stackpush.pop());
            }
        }
        return stackpop.pop();
    }

    public int peek() {
        if (stackpush.empty() && stackpop.empty()) {
            throw new RuntimeException("Queue is empty!");
        } else if (stackpop.empty()){
            while (!stackpush.empty()) {
                stackpop.push(stackpush.pop());
            }
        }
        return stackpop.peek();
    }
}

题目四 猫狗队列

题目

宠物、狗和猫的类如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public static class Pet {
    private String type;
    public Pet(String type) {
        this.type = type;
    }
    public String getPetType() {
        return this.type;
    }
}

public static class Dog extends Pet {
    public Dog() {
        super("dog");
    }
}

public static class Cat extends Pet {
    public Cat() {
        super("cat");
    }
}

实现一种狗猫队列的结构，要求如下：

  1. 用户可以调用add方法将cat类或dog类的 实例放入队列中；
  2. 用户可以调用pollAll方法，将队列中所有的实例按照进队列 的先后顺序依次弹出；
  3. 用户可以调用pollDog方法，将队列中dog类的实例按照 进队列的先后顺序依次弹出；
  4. 用户可以调用pollCat方法，将队列中cat类的实 例按照进队列的先后顺序依次弹出；
  5. 用户可以调用isEmpty方法，检查队列中是 否还有dog或cat的实例；
  6. 用户可以调用isDogEmpty方法，检查队列中是否有dog 类的实例；
  7. 用户可以调用isCatEmpty方法，检查队列中是否有cat类的实例。

实现

两个队列分别保存狗和猫；需要最早进的狗与猫这两个操作可以得以解决；

在这两个队列里保存的是包装后的狗和猫，另外包装的信息是他们进入队列的时间戳；这样对比两个队列的头部来返回最早进入队列的宠物；

对Pet的包装

有添加进入队列的时间戳；获取宠物的方法，获取时间戳的方法，获取宠物类型的方法；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public static class PetEnterQueue {
    private Pet pet;
    private long count;

    public PetEnterQueue(Pet pet, long count) {
        this.pet = pet;
        this.count = count;
    }

    public Pet getPet() {
        return this.pet;
    }

    public long getCount() {
        return this.count;
    }

    public String getEnterPetType() {
        return this.pet.getPetType();
    }
}

猫狗队列的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
public static class DogCatQueue {
    private Queue<PetEnterQueue> dogQ;
    private Queue<PetEnterQueue> catQ;
    private long count;

    public DogCatQueue() {
        this.dogQ = new LinkedList<PetEnterQueue>();
        this.catQ = new LinkedList<PetEnterQueue>();
        this.count = 0;
    }

    public void add(Pet pet) {
        if (pet.getPetType().equals("dog")) {
            this.dogQ.add(new PetEnterQueue(pet, count++));
        } else if (pet.getPetType().equals("cat")) {
            this.catQ.add(new PetEnterQueue(pet, count++));
        } else {
            throw new RuntimeException("err, not dog or cat");
        }
    }

    public Pet pollAll() {
        if (!this.dogQ.isEmpty() && !this.catQ.isEmpty()) {
            if (this.dogQ.peek().getCount() < this.catQ.peek().getCount()) {
                return this.dogQ.poll().getPet();
            } else {
                return this.catQ.poll().getPet();
            }
        } else if (!this.dogQ.isEmpty()) {
            return dogQ.poll().getPet();
        } else if (!this.catQ.isEmpty()) {
            return catQ.poll().getPet();
        } else{
            throw new RuntimeException("err, the queue is empty!");
        }
    }

    public Dog pollDog() {
        if (!this.dogQ.isEmpty()) {
            return (Dog) dogQ.poll().getPet();
        } else {
            throw new RuntimeException("err, the queue is empty!");
        }
    }

    public Cat pollCat() {
        if (!this.catQ.isEmpty()) {
            return (Cat) catQ.poll().getPet();
        } else {
            throw new RuntimeException("err, the queue is empty!");
        }
    }

    public boolean isEmpty(){
        return this.dogQ.isEmpty() && this.catQ.isEmpty();
    }

    public boolean isDogQueueEmpty() {
        return this.dogQ.isEmpty();
    }

    public boolean isCatQueueEmpty() {
        return this.catQ.isEmpty();
    }
}

题目五 转圈打印矩阵

题目

给定一个整形矩阵matrix，请按照转圈的方式打印它；

1 2 3 4

5 6 7 8

9 10 11 12

转圈打印的结果为： 1，2，3，4，8，12，11，10，9，5，6，7

要求：额外空间复杂度为 O(1)

image-20201106091549670

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
package zuoshen.basic_class.class03;

public class Code_06_PrintMatrixSpiralOrder {
    public static void spiralOrderPrint(int[][] matrix) {
        int tR = 0;
        int tC = 0;
        int dR = matrix.length - 1;
        int dC = matrix[0].length - 1;
        while (tR <= dR && tC <= dC){
            printEdge(matrix, tR++, tC++, dR--, dC--);
        }
    }

    public static void printEdge(int[][] m, int tR, int tC, int dR, int dC) {
        // 先判断边界条件
        if (tR == dR){
            for (int i = tC; i <= dC ; i++) {
                System.out.println(m[tR][i] + " ");
            }
        } else if (tC == dC){
            for (int i = tR; i <= dR ; i++) {
                System.out.println(m[i][tC] + " ");
            }
        } else{
            int curC = tC;
            int curR = tR;
            while (curC != dC){
                System.out.println(m[curR][curC++] + " ");
            }
            while (curR != dR){
                System.out.println(m[curR++][curC] + " ");
            }
            while (curC != tC) {
                System.out.println(m[curR][curC--] + " ");
            }
            while (curR != tR){
                System.out.println(m[curR--][curC] + " ");
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { {1, 2, 3, 4}, {5, 6, 7, 8 }, {9, 10, 11,12 }, {13, 14, 15,16} };
        spiralOrderPrint(matrix);
    }
}

题目六 旋转正方形矩阵

题目

【题目】 给定一个整型正方形矩阵matrix，请把该矩阵调整成 顺时针旋转90度的样子。

【要求】 额外空间复杂度为O(1)。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
package zuoshen.basic_class.class03;

public class Code_05_RotateMatrix {
    public static void rotate(int[][] matrix) {
        int tR = 0;
        int tC = 0;
        int dR = matrix.length - 1;
        int dC = matrix[0].length - 1;
        while (tR < dR){
            rotateEdge(matrix, tR++, tC++, dR--, dC--);
        }
    }

    public static void rotateEdge(int[][] m, int tR, int tC, int dR, int dC) {
        int times = dC - tC;
        int tmp = 0;
        for (int i = 0; i != times; i++) {
            tmp = m[tR][tC + i];
            m[tR][tC + i] = m[dR - i][tC];
            m[dR - i][tC] = m[dR][dC - i];
            m[dR][dC - i] = m[tR + i][dC];
            m[tR + i][dC] = tmp;
        }
    }

    public static void printMatrix(int[][] matrix) {
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                System.out.print(matrix[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 },
                { 13, 14, 15, 16 } };
        printMatrix(matrix);
        rotate(matrix);
        System.out.println("=========");
        printMatrix(matrix);
    }
}

题目七 反转单向和双向链表

题目

【题目】分别实现反转单向链表和反转双向链表的函数；

【要求】如果链表长度为N，时间复杂度要求为 $O(N)$ , 额外空间复杂度要求为 $O(1)$ ;

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
package zuoshen.basic_class.class03;

public class Code_07_ReverseList {
    // 节点类；
    public static class Node{
        public int value;
        public Node next;
        public Node(int data){
            this.value = data;
            this.next = null;
        }
    }
    // 反转链表函数
    public static Node reverseList(Node head){
        Node pre = null;
        Node tmp = null;
        while (head != null) {
            // tmp指向头节点
            tmp = head;
            // tmp拿着头节点，head向后走
            head = head.next;
            tmp.next = pre;
            pre = tmp;
        }
        return pre;
    }
    // 双向链表类
    public static class DoubleNode{
        public int value;
        public DoubleNode last;
        public DoubleNode next;

        public DoubleNode(int data){
            this.value = data;
        }
    }
    // 反转双向链表函数
    public static DoubleNode reverseList(DoubleNode head){
        DoubleNode p = head;
        DoubleNode tmp = null;
        while (p != null) {
            p.last = p.next;
            p.next = tmp;
            tmp = p;
            p = p.last;
        }
        return tmp;
    }
    // 打印链表函数
    public static void printLinkedList(Node head){
        System.out.println("Linked List: ");
        while (head != null) {
            System.out.print(head.value + " ");
            head = head.next;
        }
        System.out.println();
    }
    // 打印双向链表函数
    public static void printDoubleLinkedList(DoubleNode head){
        System.out.println("Double Linked List ");
        while (head != null) {
            System.out.print(head.value + " ");
            head = head.next;
        }
        System.out.println();
    }
    // 主函数
    public static void main(String[] args) {
        Node head1 = new Node(1);
        head1.next = new Node(2);
        head1.next.next = new Node(3);
        printLinkedList(head1);
        head1 = reverseList(head1);
        printLinkedList(head1);

        DoubleNode head2 = new DoubleNode(1);
        head2.next = new DoubleNode(2);
        head2.next.last = head2;
        head2.next.next = new DoubleNode(3);
        head2.next.next.last = head2.next;
        head2.next.next.next = new DoubleNode(4);
        head2.next.next.next.last = head2.next.next;
        printDoubleLinkedList(head2);
        printDoubleLinkedList(reverseList(head2));
    }
}

题目八 “之”字形打印矩阵

题目

image-20201110092314568

image-20201110092351277

实现

在矩阵中设计两个初始位置相同的点；

A和B分别有着不同的运动轨迹；A每次往右移动直到到矩阵的边缘再往下移动；B每次往下移动直到矩阵的边缘再往右移动

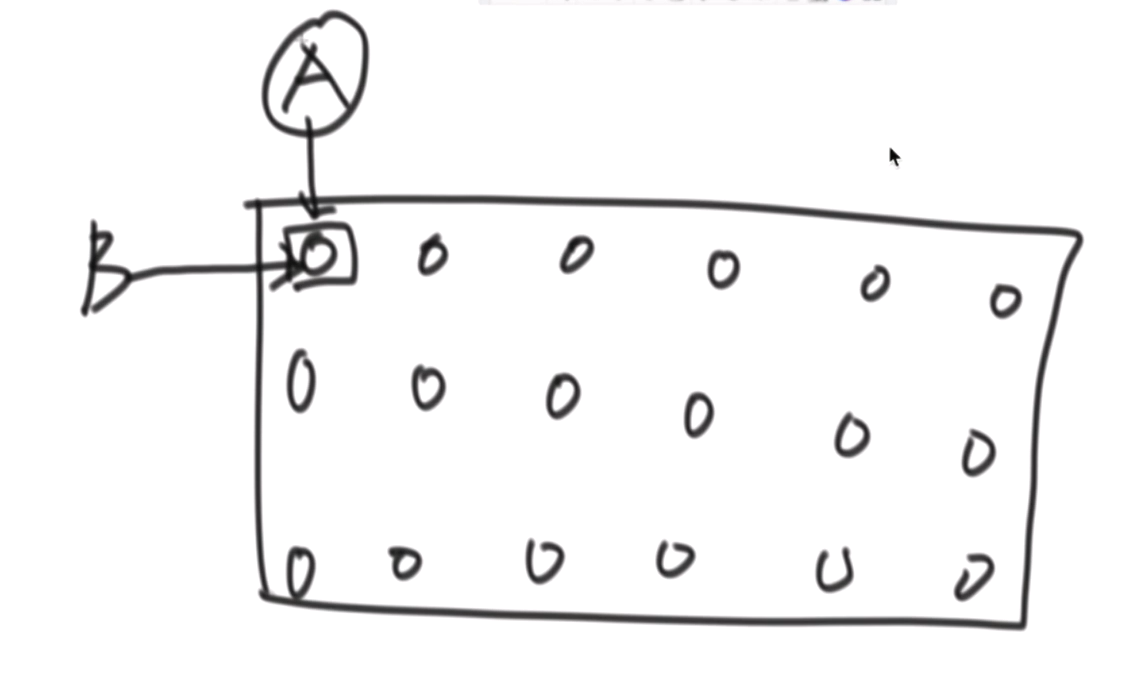
image-20201110092711246

经历过一次移动之后，A和B分别到达的位置，可以看出A和B总是处在一条线的两端：

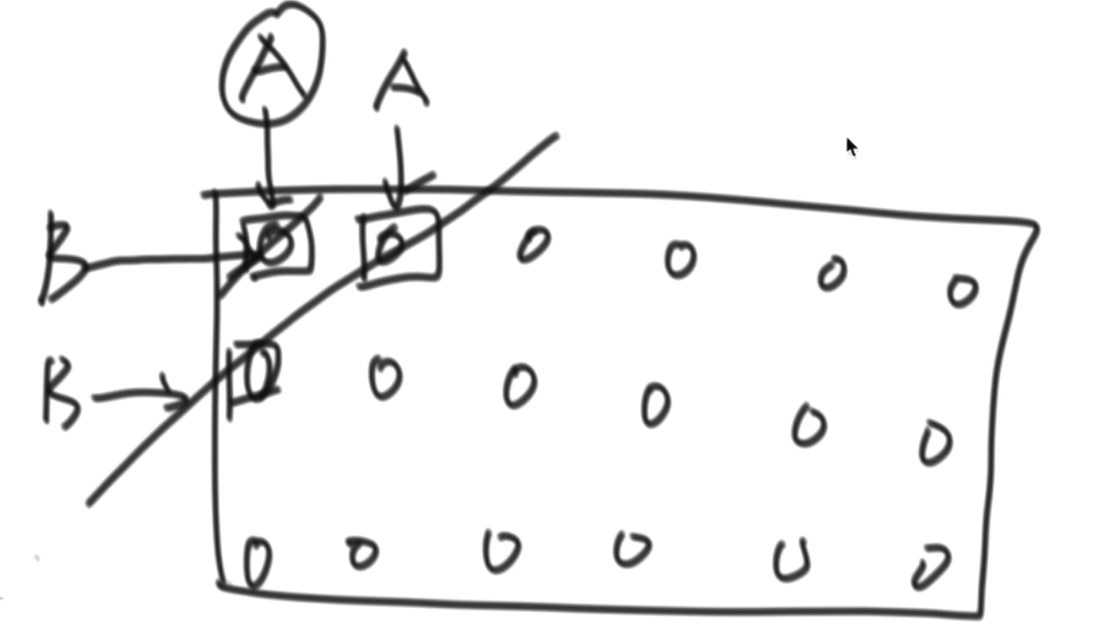
image-20201110092941055

此时B到达矩阵的边缘，开始往右走了；此时A和B仍处于一个对角线上；

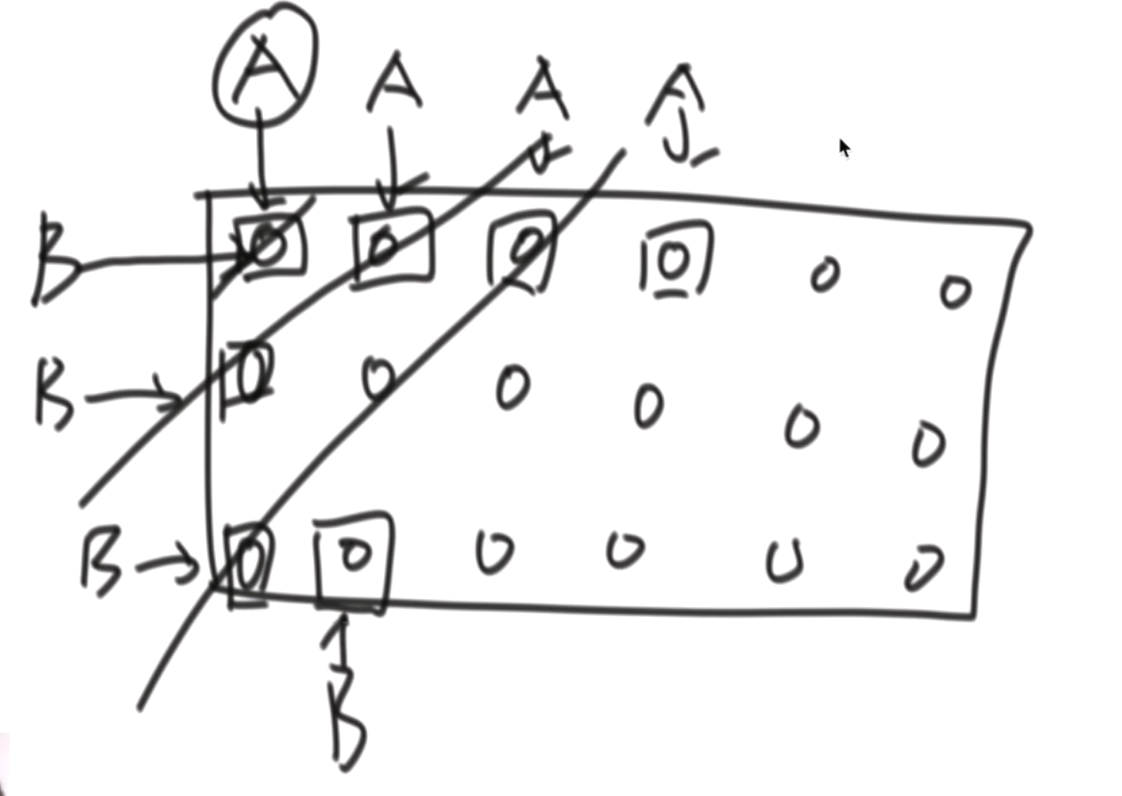
image-20201110093044928

依次类推，按顺序打印A和B所在的线，不过按照 “之” 字型打印，就需要看好是从A到B还是从B到A；需要一个布尔类型的变量来设定这件事情；

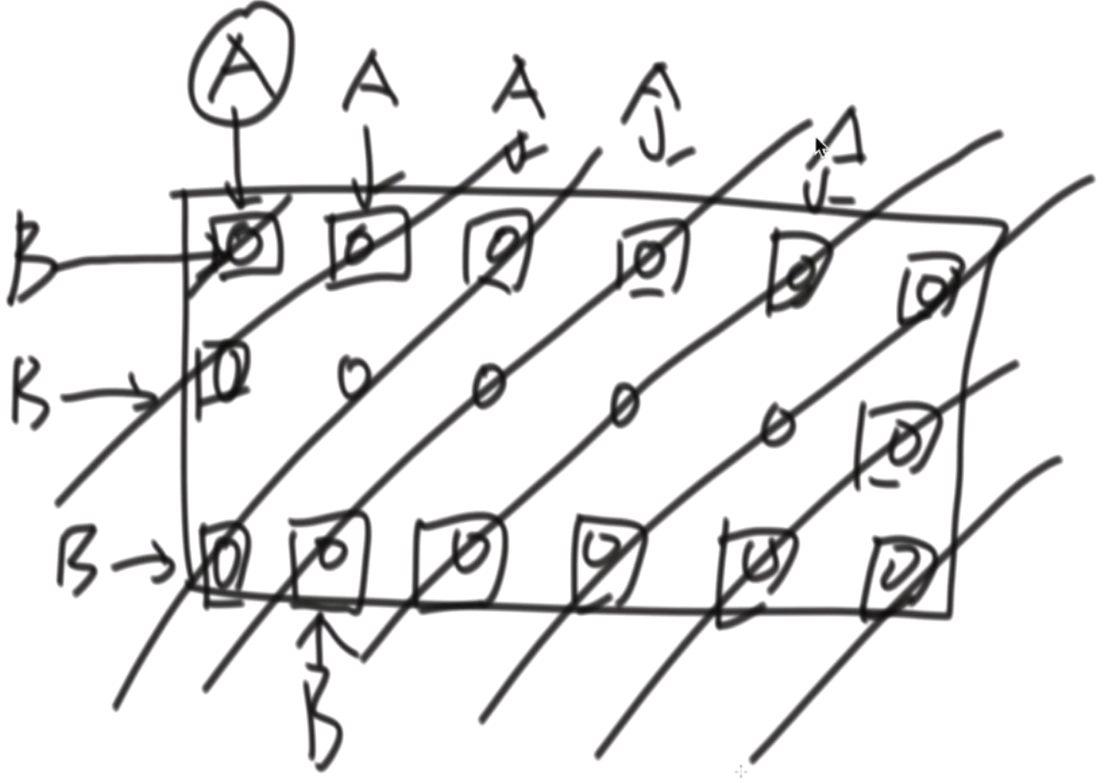
image-20201110093542635

接下来就是实现一个打印函数，这个函数需要被告知矩阵的A点和B点，然后还需要告知打印的方向；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
package zuoshen.basic_class.class03;

public class Code_07_ZigZagPrintMatrix {
    public static void printMatrixZigZag(int[][] matrix) {
        int aR = 0, bR = 0, aC = 0, bC = 0;
        int endR = matrix.length - 1;
        int endC = matrix[0].length - 1;
        boolean fromUp = false;
        while (aR != endR) {
            printLevel(matrix, aR, aC, bR, bC, fromUp);
            aR = aC == endC ? aR + 1 : aR;
            aC = aC == endC ? aC : aC + 1;
            bC = bR == endR ? bC + 1 : bC;  // 这里需要注意这几个语句的顺序；被判断的值一定是最后才修改的；
            bR = bR == endR ? bR : bR + 1;
            fromUp = !fromUp;
        }
    }

    public static void printLevel(int[][] m, int tR, int tC, int dR, int dC, boolean f) {
        if (f){
            while (tR != dR + 1) {
                System.out.println(m[tR++][tC--] + " ");
            }
        } else {
            while(dR != tR - 1) {
                System.out.println(m[dR--][dC++] + " ");
            }
        }
    }

    public static void main(String[] args) {
        int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 } };
        printMatrixZigZag(matrix);
    }
}

题目九 在行和列都排好序的矩阵中找数

题目

在行列都排好序的矩阵中找数；

给定一个有N*M的整型矩阵matrix和一个整数K， matrix的每一行和每一 列都是排好序的。

image-20201110104951864

实现

从左上角或右下角开始找，每次都能排除一行或一列的数据；

【思路】从数据状况考虑出发

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
package zuoshen.basic_class.class03;

public class Code_09_FindNumInSortedMatrix {
    public static boolean isContains(int[][] matrix, int value) {
        int row = 0;
        int col = matrix[0].length - 1;
        while (row < matrix.length && col >= 0) {
            if (matrix[row][col] == value){
                return true;
            } else if (matrix[row][col] > value) {
                col --;
            }  else {
                row ++;
            }
        }
        return false;
    }

    public static void main(String[] args) {
        int[][] matrix = new int[][] { { 0, 1, 2, 3, 4, 5, 6 },// 0
                { 10, 12, 13, 15, 16, 17, 18 },// 1
                { 23, 24, 25, 26, 27, 28, 29 },// 2
                { 44, 45, 46, 47, 48, 49, 50 },// 3
                { 65, 66, 67, 68, 69, 70, 71 },// 4
                { 96, 97, 98, 99, 100, 111, 122 },// 5
                { 166, 176, 186, 187, 190, 195, 200 },// 6
                { 233, 243, 321, 341, 356, 370, 380 } // 7
        };
        int K = 233;
        System.out.println(isContains(matrix, K));
    }
}

题目十 打印两个有序链表的公共部分

题目

给定两个有序链表的头指针head1和head2，打印两个链表的公共部分

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
package zuoshen.basic_class.class03;

public class Code_10_PrintCommonPart {
    // 需要一个节点类；
    public static class Node {
        public int value;
        public Node next;
        public Node(int data) {
            this.value = data;
        }
    }

    public static void printCommonPart(Node head1, Node head2) {
        System.out.print("Common Part:  ");
        while (head1 != null && head2 != null) {
            if (head1.value > head2.value) {
                head2 = head2.next;
            } else if(head1.value < head2.value) {
                head1 = head1.next;
            } else {
                System.out.print(head1.value + " ");
                head1 = head1.next;
                head2 = head2.next;
            }
        }
        System.out.println();
    }
    // 打印链表函数
    public static void printLinkedList(Node head){
        System.out.println("Linked List: ");
        while (head != null) {
            System.out.print(head.value + " ");
            head = head.next;
        }
        System.out.println();
    }

    public static void main(String[] args) {
        Node node1 = new Node(2);
        node1.next = new Node(3);
        node1.next.next = new Node(5);
        node1.next.next.next = new Node(6);

        Node node2 = new Node(1);
        node2.next = new Node(2);
        node2.next.next = new Node(5);
        node2.next.next.next = new Node(7);
        node2.next.next.next.next = new Node(8);

        printLinkedList(node1);
        printLinkedList(node2);
        printCommonPart(node1, node2);
    }
}

题目十一 判断一个链表是否为回文结构

题目

image-20201110110900046

实现

思路一：一个长度与链表一样长的栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// need n extra space 一个长度与链表一样长的栈；
public static boolean isPalindrome1(Node head) {
    Stack<Node> nodes = new Stack<Node>();
    Node cur = head;
    while (cur != null) {
        nodes.push(cur);
        cur = cur.next;
    }
    while (head != null){
        if (nodes.pop().value != head.value){
            return false;
        }
        head = head.next;
    }
    return true;
}

思路二：快慢指针 + 栈 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// need n/2 extra space
public static boolean isPalindrome2(Node head) {
    if (head == null || head.next == null){
        return true;
    }
    Node fast = head, slow = head;
    while (fast.next != null) {
        slow = slow.next;
        fast = fast.next.next != null ? fast.next.next : fast.next;
    }
    Stack<Node> nodes = new Stack<Node>();
    while (slow != null) {
        nodes.push(slow);
        slow = slow.next;
    }
    while (!nodes.isEmpty()){
        if (nodes.pop().value != head.value) {
            return false;
        }
        head = head.next;
    }
    return true;
}

思路三：快慢指针，快指针走两步，慢指针走一步；（其实这个方法也是找到链表中心点的方法）

  • 快指针每次走两步直到末尾，此时慢指针指向中心
    • 当链表节点个数为偶数时，慢指针刚好指向第 $\frac{N}{2}$ 的位置
    • 当链表节点个数为奇数时，快指针会移动 $\frac{N+1}{2}$ 次，慢指针也会移动 $\frac{N+1}{2}$ 次（比被2整数结果后面的一个，例如：N=5，那么移动三次指向第4个节点；N=9，移动5次指向第6个节点）；
  • 然后把慢指针之后的链表逆序；
  • 与头节点开始与慢指针比较是否是回文结构；
  • 然后恢复原链表结构；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// need O(1) extra space
public static boolean isPalindrome3(Node head) {
    if (head == null || head.next == null){
        return true;
    }
    Node fast = head, slow = head;
    while ( fast.next != null && fast.next.next !=null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    Node tmp = null;
    fast = null;
    while (slow != null) {
        tmp = slow;
        slow = slow.next;
        tmp.next = fast;
        fast = tmp;
    }
    // 分别从head 和 fast出发查看是否一样
    slow = head;    //  保存头节点
    tmp = fast; // 保存最后一个节点
    boolean res = true;
    while (fast != null && slow != null) {
        if (fast.value != slow.value){
            res = false;
        }
        fast = fast.next;
        slow = slow.next;
    }
    // 复原链表
    fast = tmp.next;    // 保存最后一个节点最后一个值
    tmp.next = null;
    while (fast != null) {
        slow = fast;
        fast = fast.next;
        slow.next = tmp;
        tmp = slow;
    }
    return res;
}

题目十二 将单向链表按某值划分成左边小、中间相等、右边大的形式

题目

【题目】 给定一个单向链表的头节点head，节点的值类型是整型，再给定一个整数pivot。实现一个调整链表的函数，将链表调整为左部分都是值小于 pivot 的节点，中间部分都是值等于pivot的节点，右部分都是值大于 pivot的节点。 除这个要求外，对调整后的节点顺序没有更多的要求。 例如：链表9->0->4->5- >1，pivot=3。调整后链表可以是1->0->4->9->5，也可以是0->1->9->5->4。总 之，满 足左部分都是小于3的节点，中间部分都是等于3的节点（本例中这个部 分为空），右部分都是大于3的节点即可。对某部分内部的节点顺序不做要求。

【进阶】在原问题的要求之上再增加如下两个要求。 在左、中、右三个部分的内部也做顺序要求，要求每部分里的节点从左到右的 顺序与原链表中节点的先后次序一致。 例如：链表9->0->4->5->1，pivot=3。 调整后的链表是0->1->9->4->5。 在满足原问题要求的同时，左部分节点从左到 右为0、1。在原链表中也 是先出现0，后出现1；中间部分在本例中为空，不再 讨论；右部分节点 从左到右为9、4、5。在原链表中也是先出现9，然后出现4， 最后出现5。 如果链表长度为N，时间复杂度请达到O(N)，额外空间复杂度请达到O(1)。

实现

思路一：把链表套进一个数组当中；数组的元素就是链表的节点；然后用荷兰国旗问题进行解决；这样子的解决方案是不能达到稳定性要求的；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public static Node listPartition1(Node head, int pivot) {
    if (head == null) {
        return head;
    }
    Node cur = head;
    int i = 0;
    while (cur != null){
        i ++;
        cur = cur.next;
    }
    Node[] nodearr = new Node[i];
    cur = head;
    for (i = 0; i < nodearr.length ; i++) {
        nodearr[i] = cur;
        cur = cur.next;
    }
    arrPartition(nodearr, pivot);
    for (i = 1; i < nodearr.length; i++) {
        nodearr[i-1].next = nodearr[i];
    }
    nodearr[i - 1].next = null;
    return nodearr[0];
}
public static void arrPartition(Node[] nodeArr, int pivot) {
    int small = -1;
    int big = nodeArr.length;
    int index = 0;
    while (index < big) {
        if (nodeArr[index].value < pivot) {
            swap(nodeArr, index++, ++small);
        } else if (nodeArr[index].value == pivot){
            index ++;
        } else {
            swap(nodeArr,index, --big);
        }
    }
}

public static void swap(Node[] nodeArr, int a, int b) {
    Node tmp = nodeArr[a];
    nodeArr[a] = nodeArr[b];
    nodeArr[b] = tmp;
}

思路二：

  • 用分别准备三个链表变量分别保存小于，等于和大于的组；

    每个链表需要两个变量保存头和尾

  • 然后把三个链表串起来就可以实现；

    需要判断每个链表是否存在，涉及一个较为复杂的编程过程；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
public static Node listPartition2(Node head, int pivot) {
    Node sH = null; // small head
    Node sT = null; // small tail
    Node eH = null; // equal head
    Node eT = null; // equal tail
    Node bH = null; // big head
    Node bT = null; // big tail
    Node cur = null;
    while (head != null) {
        cur = head;
        head = head.next;
        cur.next = null;
        if (cur.value < pivot) {
            if (sH == null) {
                sH = cur;
                sT = cur;
            } else {
                sT.next = cur;
                sT = cur;
            }
        } else if (cur.value == pivot) {
            if (eH == null) {
                eH = cur;
                eT = cur;
            } else {
                eT.next = cur;
                eT = cur;
            }
        } else {
            if (bH == null) {
                bH = cur;
                bT = cur;
            } else {
                bT.next = cur;
                bT = cur;
            }
        }

    }
    // small and equal reconnect
    if (sT != null) {
        sT.next = eH;
        eT = eT == null ? sT : eT;
    }

    if (eT != null) {
        eT.next = bH;
    }
    return sH != null ? sH : eH != null ? eH : bH;
}

题目十三 复制含有随机指针的链表

题目

【题目】 一种特殊的链表节点类描述如下：

1
2
3
4
5
6
7
8
public class Node { 
    public int value; 
    public Node next; 
    public Node rand; 
    public Node(int data) { 
        this.value = data; 
    } 
}

Node类中的value是节点值，next指针和正常单链表中next指针的意义 一 样，都指向下一个节点，rand指针是Node类中新增的指针，这个指针可能指向链表中的任意一个节点，也可能指向null。给定一个由 Node节点类型组成的无环单链表的头节点head，请实现一个函数完成这个链表中所有结构的复制，并返回复制的新链表的头节点。

进阶： 不使用额外的数据结构，只用有限几个变量，且在时间复杂度为 $O(N)$ 内完成原问题要实现的函数。

实现

【我的考虑】：直接复制相对应的节点把他们的节点的值和next 指针复制好。接着问题出现了 rand 是无法复制的。要找到第一个节点的 rand 指针需要和原始链表一样去同步遍历才能找到。这样无疑会有很大的时间复杂度；

【解法一】把原始链表与新链表通过哈希表的方式来建立联系

哈希表中的 key 是原始链表中的节点，相对应的 value 是它复制后的节点。要找到新链表节点的 next 和 rand，可以通过哈希表查找原始链表节点相对应节点来完成赋值；

【解法二】原地把原始链表与新链表关联起来：

用 $i’$ 来表示 $i$ 节点的复制节点 ，那么把它关联起来的方式是 ：

把原来的链表组织成这样的形式；每次从链表中去取出两个节点 $1 -> 1’$ ；先复制 rand 指针，$1$ 的 rand 指针可以直接找到。 而复制的新的 $1’$ 的 rand 指针可以从 $1$ 的 rand 指针找到对应节点的下一个就是 $1’$ 的 rand 指针的对应节点；

最后再把 next 指针复原组织好。即可完成；

题目十四 两个单链表相交的一系列问题

题目

【题目】 在本题中，单链表可能有环，也可能无环。

给定两个 单链表的头节点 head1和head2，这两个链表可能相交，也可能 不相交。

请实现一个函数， 如果两个链表相交，请返回相交的 第一个节点；

如果不相交，返回null 即可。

要求：如果链表1 的长度为N，链表2的长度为M，时间复杂度请达到 O(N+M)，额外 空间复杂度请达到O(1)。

实现

【我的考虑】

  1. 先分类考虑

    有环相交，有环不相交，无环相交，无环不相交

    然后发现任何一个都很复杂；

问题一 如何判断链表有没有环

​ 【方法一】哈希表

​ 通过一个哈希表，遍历链表节点；每遍历一个节点如果它不在集合中就把它放集合当中；如果第一个发现在集合中的节点，那就说明这是链表的环的入口；如果判断到节点为空，则说明不存在环；

​ 实现 : 判断一个链表是否有环，如果有，则返回环的第一个节点；没有则返回空；

​ 【方法二】快慢指针

  • 快指针走两步，慢指针走一步；

  • 直到相遇；

  • 如果相遇，快指针回到开头，由一次走两步变为一次走一步，【结论】快指针与慢指针一定会在入环节点处相遇；

问题二 如何判断一个无环单链表第一个相交的节点

由问题一我们可以知道是否有环，则可以考虑两个链表调用了判断是否有环函数后都返回为空，这个情况下他们是否有相交的节点

​ 【方法一】哈希表

​ 同样是用一个哈希表；遍历第一个链表节点，都放入哈希表当中去。

​ 然后依次遍历第二个链表，在哈希表中查。如果都没有，说明它们不相交；如果第二个链表的节点在哈希表中出现了，则说明这个节点是相交节点；

​ 【方法二】

​ 遍历第一个链表，得到他的长度与最后一个节点的指针；同样的遍历第二个链表，得到他的长度和最后一个节点的指针；

  • 显而易见：判断 两个链表的最后一个节点是否是一个节点即可判断他们是否相交；
  • 如果它们相交，根据链表长度去遍历；
    • 让长的链表先走，走到与短的一样长时它们一起走。
    • 然后判断两个链表当下节点是否一样，直到它们指向节点一样也就是找到了相交的第一个节点；

问题三 如何判断一个有环单链表与无环单链表第一个相交的节点

​ 不可能相交；

问题四 如何判断两个有环单链表第一个相交的节点

三种情况：

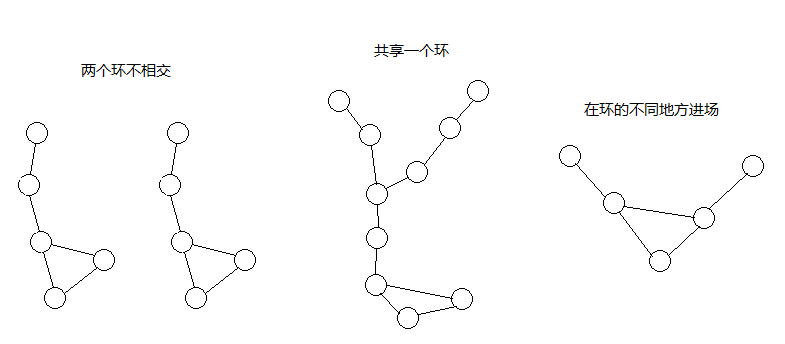
image-20201119153209312

  • 如果判断是有环并且得到的入环节点位置相同，他就是结构2：
    • 此时也就等同于无环链表相交，此时相交位置与入环节点没有关系；
  • 如果入环节点不相同，他可能是结构1也可能是结构2：
    • 此时从链表一的入环节点出发，遍历链表；
      • 如果碰到链表二的入环节点：则说明是第三种结构
        • 此时返回链表一的入环节点和链表二的入环节点都是对的；
      • 如果链表一的入环节点遍历回去了，还没碰到说明是结构一；
        • 不存在相交节点；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
public static Node getIntersectNode(Node head1, Node head2) {
    if (head1 == null || head2 == null) {
        return null;
    }
    Node loop1 = getLoopNode(head1);
    Node loop2 = getLoopNode(head2);
    if (loop1 == null && loop2 == null) {
        return noLoop(head1, head2);
    } else if (loop1 != null && loop2 != null) {
        return bothLoop(head1, loop1, head2, loop2);
    }
    return null;

}

public static Node getLoopNode(Node head) {
    if (head == null || head.next == null || head.next.next == null) {
        return null;
    }
    Node n1 = head.next;
    Node n2 = head.next.next;
    while (n1 != n2) {
        if (n2.next == null || n2.next.next == null) {
            return null;
        }
        n1 = n1.next;
        n2 = n2.next.next;
    }
    n2 = head;
    while (n1 != n2) {
        n1 = n1.next;
        n2 = n2.next;
    }
    return n1;
}

public static Node noLoop(Node head1, Node head2) {
    if (head1 == null || head2 == null) {
        return null;
    }
    Node cur1 = head1;
    Node cur2 = head2;
    int n = 0;
    while (cur1.next != null) {
        n ++;
        cur1 = cur1.next;
    }
    while (cur2.next != null) {
        n --;
        cur2 = cur2.next;
    }
    if (cur1 != cur2) {
        return null;
    }
    cur1 = n > 0 ? head1 : head2; // cur1 指向较长的链表
    cur2 = cur1 == head1 ? head2 : head1; // cur2 指向另一个
    n = Math.abs(n);
    while (n != 0) {
        n --;
        cur1 = cur1.next;
    }
    // cur1 和 cur2 同时出发
    while (cur1 != cur2) {
        cur1 = cur1.next;
        cur2 = cur2.next;
    }
    return cur1;
}

public static Node bothLoop(Node head1, Node loop1, Node head2, Node loop2) {
    if (head1 == null || head2 == null) {
        return null;
    }
    Node cur1 = null;
    Node cur2 = null;
    if (loop1 == loop2) {
        cur1 = head1;
        cur2 = head2;
        int n = 0;
        while (cur1 != loop1) {
            n ++;
            cur1 = cur1.next;
        }
        while (cur2 != loop2) {
            n --;
            cur2 = cur2.next;
        }
        cur1 = n > 0 ? head1 : head2; // cur1 指向较长的链表
        cur2 = cur1 == head1 ? head2 : head1; // cur2 指向另一个
        n = Math.abs(n);
        while (n != 0) {
            n --;
            cur1 = cur1.next;
        }
        // cur1 和 cur2 同时出发
        while (cur1 != cur2) {
            cur1 = cur1.next;
            cur2 = cur2.next;
        }
        return cur1;
    } else {
        cur1 = loop1.next;
        while (cur1 != loop1) {
            if (cur1 == loop2) {
                return loop1;
            }
            cur1 = cur1.next;
        }
        return null;
    }
}