排序

冒泡排序

每次把当前数组最大值通过交换放到最后；时间复杂度：$O(N^2)$

对这个算法描述分为三个层面

宏观： 用end控制前面数组中的最大值存放的位置；它的初始值为N-1，结束值为1；
中层： 把0 ~ end里的最大值传递到end位置；
微观： 从`0 ~ end-1` 针对于相邻两个元素进行比较（位置0 和 位置1 比较； 然后位置1 和 位置2 比较；直到位置end-1 和 位置end 比较；）；
	  前面的大于后面的则交换;

微观层面的算法是对中层的具体实现；中层又是宏观中的一部分；

选择排序

0 ~ N-1范围内找到最小的放在 0 位置

1 ~ N-1范围内找到最小的放在 1 位置

2 ~ N-1范围内找到最小的放在 2 位置

每次找到i ~ N-1位置里的最小值的下标，与i位置进行交换。

1
2
3

1： 第 i 位置后的最小值放在 i 位置；于是 i 取值范围为 0 ~ N-2 ； （因为 N - 1 之后没有数了， 也就是它自己了）
2： 需要一个变量 minIndex 来保存最小值的下标；在 i ~ N-1 范围里找最小值；
3： 交换 i 位置上的数和 minIndex 上的数；

插入排序

0 ~ 0范围内的数只有一个，认为是已排序的；

0 ~ 1 范围里的数，如果判断 1 位置上的数小于 0 位置上数则进行交换，否则不交换；

0 ~ 2 范围里的数，把 2 位置上的数从后往前依次比较，如果小于则，交换，如果大于则停止；

从已排序的部分最大值往前比较，如果大与它前一个值就不交换。如果小于则与他前一个值交换。

差不多已经排序了的数组可以用插入排序。这个和数据状况有关系。完全有序O(N) ；完全逆序就是 O(N^2) ;

1： 变量 i 表示要插入数的位置； i 的范围是 1 ~ N-1
2： 要把 i 位置数插入到 0 ~ i-1 范围里面去；
3： 变量 j 表示要插入值目前的位置： 如果 j 大于 0 且 j 位置上的数小于 j-1 位置上的数， 则交换， j--； 否则停止；
    j 的范围是 1 ~ i

时间复杂度

最好情况 O(N) 最差情况 O(N^2) 平均情况 O(N) ~ O(N^2)

对数器

对数器的作用

1. 无测试样例时可以用对数器测试代码

2. 小样本测试过了，但是面对大样本测试出错，可以用对数器帮助修改bug

3. 如何证明贪心策略是对的？这是很难的。所以用对数器可以试贪心策略是对是错。

对数器的构成

1. 产生随机样本的函数

/*
	
	生成随机长度， 随机内容的数组

*/
public static int[] generateRandomArray(int size, int maxValue)

2. 一个绝对正确的方法

那么这个方法可能是来自于系统提供的；

或者是自己写的一个绝对正确但是时间复杂度过不了的方法；

3. 大样本测试

我们把自动生成的测试样例输入进 绝对正确的方法 和 想要测得方法 ；然后判断他们的输出是否一致；把这个过程重复很多次，可以是很大的值，也就是说可以也许穷尽所有的可能性；

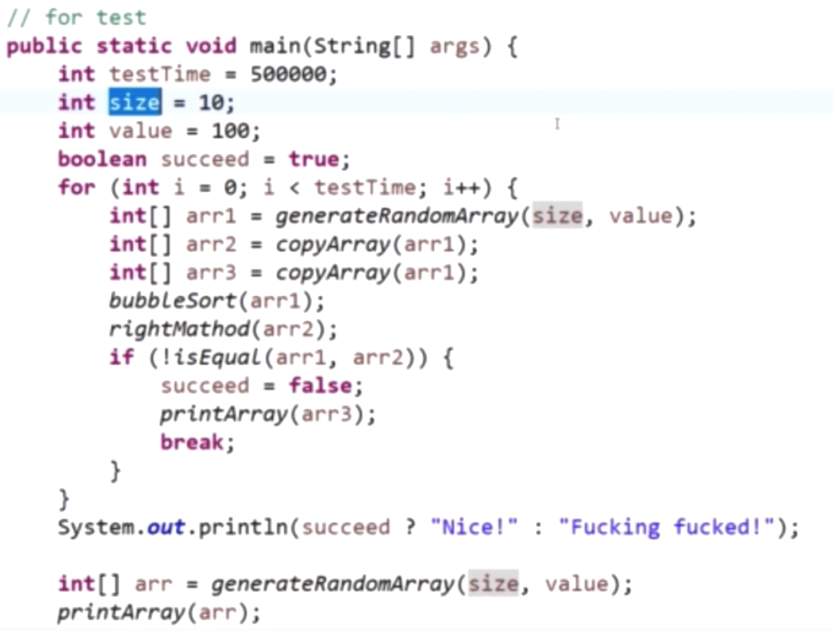
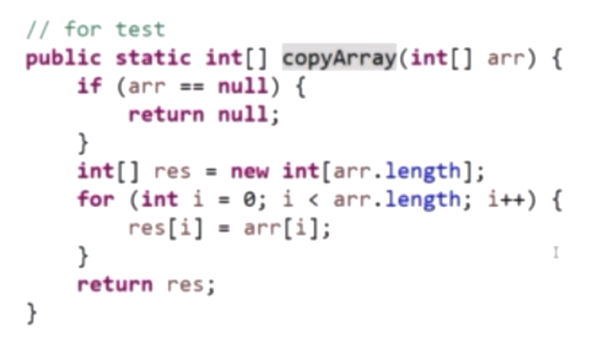
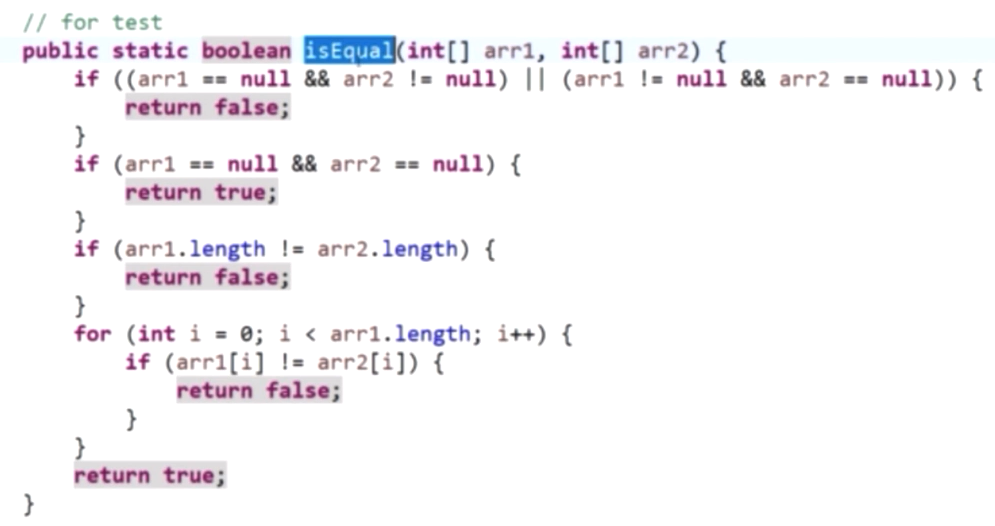
对数器的概念和使用

有一个你想要测的方法a，
实现一个绝对正确但是复杂度不好的方法b，
实现一个随机样本产生器
实现比对的方法
把方法a和方法b比对很多次来验证方法a是否正确。
如果有一个样本使得比对出错，打印样本分析是哪个方法出错；
当样本数量很多时比对测试依然正确，可以确定方法a已经正确。

笔试的时候要准备对数器

我大概想到要写一个类；然后由各种继承得到；要覆写的东西也是很多；

python的话，有使输入格式规范的包；

剖析递归行为和递归行为时间复杂度的估算

剖析递归行为

把当前运行函数压进系统栈中，保留当前函数的所有信息。调用的函数就在栈顶。

任何递归行为都可以改为非递归；

递归行为时间复杂度的估算

大部分的递归过程都可以用这个公式来表示

$T(N) = aT( \frac{N}{b} ) + O(N^d)$

$N$表示样本量，$T(N)$表示时间复杂度；那么这个复杂度分成了$a$个$T(N/b)$个子问题的过程加上一个$O(N^d)$剩余时间过程的时间；

满足这个公式的递归过程的时间复杂度的计算如下：

$T(N) = \begin{cases} O(N^{log_ba}), & {log_ba} > d \\ O(N^d*{logN}), & {log_ba} = d \\ O(N^d), & {log_ba} < d \end{cases}$

但是像$T(N)=T(\frac{N}{5})+T(\frac{2}{3}N)+O(N^2)$这样的公式就不符合上面的这个过程；

补充阅读：算法的复杂度与 Master 定理

归并排序

把一个数组分为左右两个部分。先把左侧的排好序，再把右侧的排好序。最后用外排的方式排好序。这个过程的时间复杂度是下式：

$T(N) = 2 *T(\frac{N}{2})+O(N)$

把这个公式带入到上一节，就可以查到它的时间复杂度为 $O(N*logN)$ 。并且归并排序的过程仅仅需要用到一个和原数组长度一样的数组，那么它的空间复杂度为$O(N)$

归并排序的思想

针对一个数组将其分为两个部分，分别对这两个部分用归并排序。然后对整个数组进行一个外部排序。

外部排序：针对有序的两个数组；分别用两个指针指向他们的头部。然后依次往一个辅助数组里填入两个指针中更小的值；直到两个部分都填入了辅助数组后，再把已排序好的填回原数组。

归并排序的组成部分

主函数用来对整个数组进行排序，它调用第二个组成

public static void mergeSort(int[] arr){
    if (arr == null || arr.length < 2){
        return ;
    }
    sortProcess(arr, 0, arr.length - 1);
}

对未排序的数组L到R部分的排序过程

/*
  如果L==R则范围里只有一个数，那么直接返回就好了。可以认定他是有序的；
  如果有多余一个的数则把它分为前后两部分，分别进行归并排序。然后再对这两部分进行外部排序；
*/
public static void sortProcess(int[] arr, int L, int R)

合并L到mid 和 mid+1到R两个排序好的部分：把她两排序整合到一个辅助数组里，然后再拷贝回去；

/*
	外部排序需要：一个辅助数组（大小为：R-L+1），两个指针（分别指向已排序好的两部分的头部），辅助数组下标；
	过程：
		1. 谁小填谁：进行一个循环（两个指针都不超过他们的边界的情况下），谁小就把谁填进辅助数组中；
		2. 谁没了把另一个剩下的全部填入辅助数组中：因为上一个循环已经破除则一定有且只有一个指针越界（因为每次只填入一个数，一次只可能有一个越界）
			所以这里会分别对两个指针进行判断是否到边界。他们是非此即彼的关系，即只会执行一个。
		3. 最后需要把 辅助数组拷贝回 L到R之间的位置；
*/
public static void merge(int[] arr, int L, int mid, int R)

归并排序的应用：小和问题和逆序对问题

小和问题

在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。

例子

[1,3,4,2,5] 

1左边比1小的数，没有； 

3左边比3小的数，1； 

4左边比4小的数，1、3； 

2左边比2小的数，1； 

5左边比5小的数，1、3、4、2； 

所以小和为1+1+3+1+1+3+4+2=16

注意这个题不是算一个数之前有多少比它小的个数，而是算比它小的数的和。

普通思路

这个笨办法就是进行遍历看这个数之前有几个数比它小；可以把它做对数器；

public static int comparator(int[] arr) {
    if (arr == null || arr.length < 2) {
        return 0;
    }
    int res = 0;
    for (int i = 1; i < arr.length; i++) {
        for (int j = 0; j < i; j++) {
            res += arr[j] < arr[i] ? arr[j] : 0;
        }
    }
    return res;
}

归并排序的思路

graph TD
A[1,3,4,2,5] --> B[1,3,4]
B --> D[1,3]
D --> H[1]
D --> I[3]
B --> E[4]
A --> C[2,5]
C --> F[2]
C --> G[5]
H -->|产生一个小和| J[1,3]
I -->|数字1*后面长度1| J
J -->| 数字1*长度1| K[1,3,4]
E -->| 数字3*长度1| K
F -->| 数字2*长度1| L[2,5]
G --> L
K -->|数字1*长度2 + 不产生小和| M[1,2,3,4,5]
L -->|数字3*长度1 + 数字4*长度1| M

归并排序求小和的组成部分

主函数，主要就是判断输入进来的数组是否符合规定
1
public static int smallSum(int[] arr)

归并排序求得数组小范围内的小和

1	public static int mergeSort(int[] arr, int l, int r)

合并

1	public static int merge(int[] arr, int l, int m, int r)

这里代码与归并排序都是一样的不过在比较时多了一句算小和的代码：

1	res += arr[p1] < arr[p2] ? arr[p1] * (r - p2 + 1) : 0;

逆序对问题

在一个数组中，左边的数如果比右边的数大，则折两个数构成一个逆序对，请打印所有逆序对。